Here is a problem recently described to me. Apparently there is a more elegant solution (which may give more insight), but I don’t see it yet.

The problem: \(X, Y, Z\) are independent random variables uniformly distributed over [0,1]. What is the distribution of \((XY)^Z\)?

The conventional solution is to find the distribution of \(XY\) first, then of \((XY)^Z\).

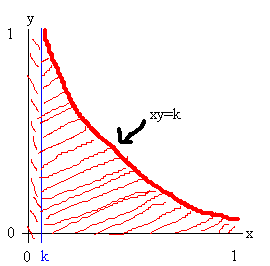
The distribution of \(XY\) can be derived from its CDF \(F_{XY}(xy \le k)\), which is the total shaded area shown. The red curve is the function \(y=\frac{k}{x}\). This area is thus given by:

\(\int_k^1 \frac{k}{x} dx + k = k \ln(x) \vert_k^1 + k = -k \ln(k) + k\), for \(k>0\).

The PDF is the derivative of the above:

\(f_{XY}(k) = -\ln(k)\), for \(k>0\). The density is not well defined at \(k=0\).

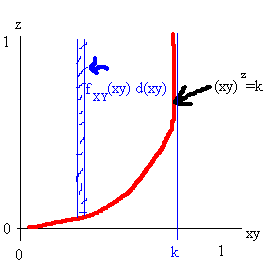
The second part is to find the distribution in question. Here, the red curve is the function \(z=\frac{\ln(k)}{\ln(xy)}\). The CDF \(F_{(XY)^Z}((xy)^z \le k)\) is the total area to the left of the red curve. A column slice shaded in blue has probability per unit of \(z\) as labeled. Thus, the CDF is:

\(\int_0^k f_{XY}(v) dv (1-\frac{\ln(k)}{\ln(v)}) = \int_0^k -\ln(v) dv (1-\frac{\ln(k)}{\ln(v)})\)
\( = \int_0^k -\ln(v) dv + \int_0^k \ln(k) dv\)
\( = -v \ln(v) + v \vert_{\downarrow 0}^k + k \ln(k) = -k \ln(k) + k + k \ln(k) = k\), for \(k>0\).

For \(k=0\), we can fill in 0, because the minimum value of \((XY)^Z\) is 0, so it is the minimum of the support of its CDF.

So amazingly, \((XY)^Z\) has the CDF of (and is) a uniform distribution. How does that happen? What’s the intuition?