Borders the “bricks-and-mortar” bookstore went bankrupt last week. After more than a decade since the first online shopping sites opened up, the physical retail store is finally taking mortal blows. Well, not all physical retail stores — some survived by successfully running their own online sites. But let’s not overly distinguish between such apparent survival and those that fail, since this mere issue of ownership doesn’t change the facts.

On the one hand, this development is a milestone triumph of digital efficiency and convenience, something I greatly appreciate. On the other hand, I — and it seems many others — can’t seem to muster the schadenfreude over the demise of a bookstore. Doesn’t seem right, but why?
(Read the article)

Comments(0)

I found the title of this article, “Honeybees might have emotions,” hard to believe. But then what is “emotion”?

Bateson and Wright tested their bees with a type of experiment designed to show whether animals are, like humans, capable of experiencing cognitive states in which ambiguous information is interpreted in negative fashion.

and from the referenced paper itself:

We show for the first time that agitated bees are more likely to classify ambiguous stimuli as predicting punishment. Shaken bees also have lower levels of hemolymph dopamine, octopamine, and serotonin.

If an “ambiguous” stimulus is one that is unassociated with anything but is interpreted as a mixture of two known stimuli (or if it is explicitly some mixture-state stimulus… is it in this case?), then isn’t all this simply risk-aversion? If so, then basically bees have concave utility like probably all evolved organisms naturally should — to stay alive. Indeed, the fact that the actual chemical signaling mechanism for risk-aversion is associated with “pessimism” or “depression” in higher organisms is the more intriguing (but on second thought, obvious) result, suggesting that emotions are just internal (psychological) reward adjustments that drive external (behavioral) risk adjustments. Emotions bend the utility “function” into shape by applying compensatory rewards to the actual external rewards: a risk and reward add-on circuit.

Comments(0)

Something in the news here today, referring also to Penrose’s paper from several years ago.

In my limited understanding, Penrose suggests that the universe goes through these cycles of what can be interpreted as infinite expansions “followed by” big bangs, where the cycle renewal “happens” in a mathematical sense: in the way spacetime is metrized. He says that in the infinite future, when all massive particles will have evaporated, we will be returned to a situation without a notion of space or time (since all things are lightlike, I suppose). From this, the very large scale of the given final universe can be reinterpreted as the very small beginning of the next universe. It’s an interesting thought.

Comments(0)

Scientists create synthetic cell, version 1.0 | [paper]

Our synthetic genomic approach stands in sharp contrast to a variety of other approaches to genome engineering that modify natural genomes by introducing multiple insertions, substitutions, or deletions (18–22). This work provides a proof of principle for producing cells based upon genome sequences designed in the computer. DNA sequencing of a cellular genome allows storage of the genetic instructions for life as a digital file.

This seems significant, equivalent to booting up the first stored-program computer.

Scientists who were not involved in the study are cautioning that the new species is not a truly synthetic life form because its genome was put into an existing cell.

That’s sour grapes, because the original cell cytoplasm decays to zero exponentially fast in the number of replications, a point well made in the paper. It’s only needed for booting. What’s more useful to know is how much of the 1.08Mbp genome consists of existing genes. The paper says it’s a close copy of M. mycoides:

The synthetic genome described in this paper has only limited modifications from the naturally occurring M. mycoides genome. However, the approach we have developed should be applicable to the synthesis and transplantation of more.

The next step will be a basic cell with a minimal genome, a barebones cell OS, if you will. Then, on to synthetic functions. Pretty soon we’ll have cell API’s, fancy-pants programming frameworks, and bugs and viruses. I mean real ones.

Comments(0)

Big bang an exploding white hole, opposite of a black hole? (paper) This sounds interesting and somehow satisfying.

LED light bulbs coming, but incandescents being phased out by mandate in January, 2012? What?! Time to stockpile bulbs. I like my black-body radiation.

Speaking of black-body radiation, suppose I have an enclosed system with a single aperture for light and only light to pass through. Do I now have a system for converting heat to light, and therefore to electricity via bandgaps? Doesn’t that violate some law of thermodynamics?
(Read the article)

Comments(0)

There was a talk today that referenced this paper by Banerjee, El Ghaoui, and d’Aspremont on obtaining sparse graphical models for parameterized distributions.

This undirected graphical model stating conditional independence relationships of senate voting behavior was shown.

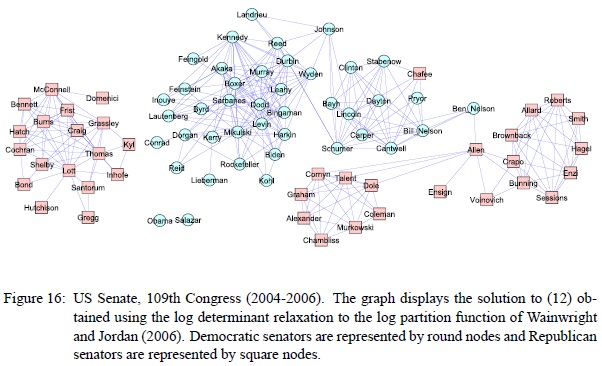
If two nodes A and B are connected only through a set of nodes C, then A and B are independent, conditioned on C. Basically it says if you want to predict anything about B from A and C, then C is enough, because A won’t tell you anything more. As pretty as the graph looks, this is a rather odd visualization. Without seeing the (Ising) model parameters, especially where the edge weights are positive or negative, this graph is hard to interpret, and the conclusions in the paper are especially questionable to me. In particular, being in the middle of this graph does not necessarily imply “moderation” or “independence”, (unlike in let’s say this graph). We would expect moderates to exhibit weak dependency to either party’s large cliques. But if, for example, the edge weight between Allen and B. Nelson is a strongly negative one (which it very well may be, since the two parties are not otherwise connected via negatively weighted edges), then the graph seems to imply that how the two parties vote can largely be predicted from the votes of the likes of Allen or B. Nelson; in that sense, they are the indicators for their parties, disagreeing on exactly those party-disambiguating issues.

There is some additional funny stuff going on. According to the paper, a missing vote counts as a “no” because they only solved the problem for binary and Gaussian distributions. I also count only about 80 nodes in there, while there are 100 senators. The graph structure also seems a bit too sparse, but this may be intentional, in order to drop weak dependencies from the graph. One does wonder though, whether the results weren’t really that good without manual fudging.

Unrelatedly, this reminds me of another famous academic paper graph, the high school dating graph:

If you look carefully, there is some oddball stuff going on here, too.

Comments(0)

There have long been Middle Chinese and Old Chinese reconstructions on paper, but since the Chinese script is not phonetic (although syllabic to a degree), it has been difficult to ascertain pronunciations. If one takes Classical Latin as an example — that is a reconstruction of fairly normal and believable speech of about 2000 years ago if read aloud, yet there is nothing approaching that for Middle Chinese (about >1000 years ago) much less for Old Chinese (>2000 years ago). Recently though, a couple of funny videos cropped up on Youtube showing people making overly academic attempts at reading classical texts using reconstructed archaic pronunications.
(Read the article)

Comments(0)

Because this article is spamming the internet today, I decided to read Li’s paper and learn what the heck is this Gaussian copula.

For five years, Li’s formula, known as a Gaussian copula function, looked like an unambiguously positive breakthrough, a piece of financial technology that allowed hugely complex risks to be modeled with more ease and accuracy than ever before. With his brilliant spark of mathematical legerdemain, Li made it possible for traders to sell vast quantities of new securities, expanding financial markets to unimaginable levels.

And anyway, here is the paper referenced in the article.
(Read the article)

Comments(2)

I suppose good penmanship is the basis of good calligraphy, since calligraphy is mainly the addition of (variable) brush width to the structure of the characters. This bulk structure is really the key and it is particularly difficult to get correctly without muscle memory. That’s why they tell you to trace character books over and over.

However, there is a way to figure this matter of structure from first principles (and perhaps generate a more unique style as a result), albeit with the tradeoff that you cannot be quick, you must be careful.
(Read the article)

Comments(0)

Now that I have gotten seriously addicted to Tablet PC (the faux paper templates in Windows Journal alone were enough to get me hooked), I’ve been pondering about some limitations of the platform. One is authentication. One of things you are not happy to do with a mouse — which the pen is, sort of — is inputting random strings that have become of modern-day passwords.

So I understood the point of the fingerprint reader option on this build. Swipe and you can bypass having to type passwords in tablet mode when the keyboard is hidden. But I didn’t get the option, and I believe there are other alternatives.

There are many modes of biometric authentication, fingerprint, face recognition, handwriting, voice, etc., and getting nearly perfect reliability in each case is a difficult problem when used alone. State of the art is just not good enough. But combined into a multifactored authentication protocol, it may just work. Here is something that should work today with existing hardware:

That should do the trick for a quick keyboard-less authentication. Why hasn’t anybody written software to do this?

Comments(0)