Suppose there is a straight road, infinitely long at both ends, located 1 unit from your starting location. Find the most efficient path to reach the road, and the worst-case total length of this path.

The trivial but wrong way is to go for 1 unit in some direction, then trace the circumference of a unit-radius circle. The road will surely be found this way, but the path length is \(1+2\pi\), which can be improved upon.

Every possible position for the road corresponds to a tangent line to the unit circle centered at the starting location. Therefore, this is a problem about finding a shortest path that touches all tangent lines to a unit circle. To make this more concrete, let us transform the space into polar form as below.

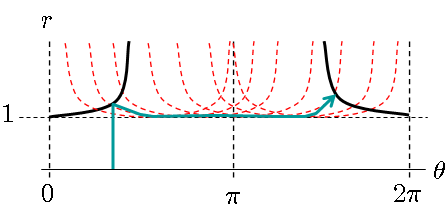
We see that in polar form, the unit circle becomes the line \(r=1\) and each tangent line touching the circle at angle \(\theta_0\) becomes the graph \(r=\sec(\theta-\theta_0)\). The trivial solution corresponds to a path that traces \(r=0\) to \(r=1\) at \(\theta=0\), followed by \(\theta=0\) to \(\theta=2\pi\) at \(r=1\). This is not efficient.

In fact, any continuous path starting at \(r=0\) “reaches the road” (i.e. touches every tangent line) as long as it touches \(r=\sec(\theta)\) somewhere on \(\theta\in [0,\pi/2)\) and somewhere on \(\theta\in (3\pi/2,2\pi]\), and it stays above \(r=1\) between those two points. And up to shifts in \(\theta\), these are the only possible solutions.* Note that the path doesn’t need to be closed, like the trivial path was. So we are left to find the shortest such path (e.g. the one in green above).

Whereas in rectangular form, the shortest path between two points is a straight line, in polar form, the shortest path between two points is along a secant graph. It is a fairly easy matter to show that the shortest path must take the following form:

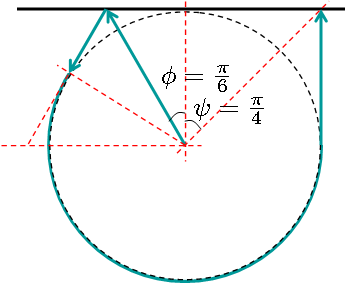
1. Start from \((r,\theta)=(0,\phi)\) for some \(\phi\in [0,\pi/2)\);
2. Drop onto the graph \(r=\sec(\theta-2\phi)\), between the points \((r,\theta)=(\sec(\phi),\phi)\) and \((r,\theta)=(1,2\phi)\);
3. Take the path \(r=1\) from \(\theta=2\phi\) to some \(\theta=2\pi-2\psi\);
4. Drop onto the graph \(r=\sec(\theta-(2\pi-2\psi))\), between the points \((r,\theta)=(1,2\pi-2\psi)\) and \((r,\theta)=(\sec(2\pi-\psi),2\pi-\psi)\).

Finally, we need to solve two minimizations, which will find the best \(\phi\) and \(\psi\). \(\psi\) can actually be solved by inspection, but formally:

\(\min_{\psi\in[0,\pi/2)} \tan(\psi) + \pi - 2\psi\)
solution at \(\sec^2{\psi} = 2 \Rightarrow \psi=\pi/4\)

\(\min_{\phi\in[0,\pi/2)} \sec(\phi) + \tan(\phi) + \pi - 2\phi\)
solution at \(\frac{\sin(\phi)}{\cos^2(\phi)} + \sec^2(\phi) = 2 \Rightarrow \sin(\phi)=1/2 \Rightarrow \phi=\pi/6\).

The solved path has total length \(\tan(\pi/4) + \pi – \pi/2 + \sec(\pi/6) + \tan(\pi/6) + \pi – \pi/3 = 1+\sqrt{3}+7\pi/6\), and is plotted below. This is about 12% shorter than the trivial path.

---

* Technically, we still need to prove that paths that re-enter the unit circle (go below \(r=1\)) are not worthy. One can reason about why such paths can be improved upon by replacing the path segments that re-enter the unit circle, but it seems a proof needs some global properties of the path. With the reader comment (below) about reflecting the starting point, the best path actually becomes a function \(r(\theta)\), of the variable \(\theta\), which almost certainly is a necessary condition for efficient paths. Then we can impose other constraints, like, \(\forall \theta_0: r(\theta) \not< \sec(\theta-\theta_0)\), which says the path function should not be dominated by any secant function (equivalent to crossing all tangent lines to the unit circle). This may be a direction to a complete proof.