I’ve been meaning to learn the game of “Go” (weiqi) for quite a while now, and finally got around to it now that there are some people at Harvard at beginner’s levels to play with.

The usual adage is that the rules of “Go” are simple, but the strategies are difficult. Sometimes they cite the fact that computers can’t play “Go” very well (compared to, say, chess). I’m not in a position to defend or refute this sentiment yet, but I think this stuff is easier than it first appeared to me years ago, if you think about it the right way. “Go” seems a very mathematical game, almost a counting and topological reasoning game. And all the difficulties arise out of the fact that the counting and reasoning is done in 2D (rather than 1D, which would be simple).

So there is this list of terminology like “liberties,” “eyes,” “false eyes,” “alive and dead regions,” etc., but sometimes they greatly confuse the matter, so I found it easier to recast these basic concepts in more general terms.

There are really only two axiomatic rules to play Go.

Def. 1: A group of stones is some stones of the same color.
Def. 2: A liberty of a group is any of the cardinal neighbor points of the stones in the group that is unfilled.
Rule 1: A group can be captured if all the liberties of the group are filled by the opposing color.
Rule 2: A point that when filled would result in an immediate capture of a group to which the point also belongs cannot be filled, unless it results in a capture of a group of the opposing color and if in the immediate previous move it was not itself captured.

Of course, nobody plays “Go” using only axioms. Instead we use the axioms and properties of the board* to derive new results:

I. The concept of an “alive group” by means of forming “two eyes.” This group of black stones is said to be alive idiomatically because it has “two eyes.” Well, turns out the real proposition is this:
Def. 3: A “connected group” is a group for which there exists no subgroup with all the liberties unfilled by a stone of the same color. (We’re neglecting some issues related to stones on edges and corners.)
Prop. 1: A connected group must be captured together.
Proof: To capture any subgroup of the connected group, its liberties must be taken, but some of its liberties is occupied by a same-color stone not belonging to the subgroup, therefore the subgroup cannot be taken. Since all subgroups of a connected group are like this, no subgroup of a connected group can be captured alone.
Def. 4: An “eye” is a minimal subgroup of a connected group that, if alone on the board, has exactly one liberty for which filling it would trigger Rule 2. To “fill” an eye is to fill all its liberties.
Prop. 2: A connected group with two or more “eyes” cannot be captured.
Proof: Each player can only make one move per turn, and therefore two or more “eyes” cannot be filled simultaneously. Then each eye in the group must be filled separately, in some order. But that would involve invoking Rule 2 at some point for the first of these eyes, when none of the other eyes have been filled. Since the group is connected, it must be captured together, yet we just said it does not have all of its liberties filled at the time that Rule 2 is invoked, and therefore filling the first eye is an unallowed move. Therefore, a connected group with two or more “eyes” cannot be captured.

II. Next, the “false eye” is simple, like the top one here. It’s just not an eye by Def. 4, since the circled black stone and the one above it are not in a connected group with the rest of the black stones.

Corollary 1: A group that is a disjoint union of connected subgroups cannot be captured if each subgroup has two or more liberties that would trigger Rule 2.
(Formations around these liberties are also called “eyes” usually, but I don’t consider them eyes.)

III. Usually the next step is learning how some groups that don’t have two or more eyes are nevertheless “alive,” “dead,” or “unsettled” based on how further moves could necessarily, necessarily not, or possibly — dependent on move order — allow the capture of the group. This is usually part of some rote memorization drill in Go, but it doesn’t have to be this way.

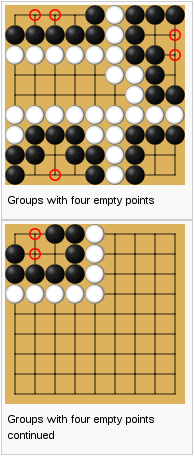
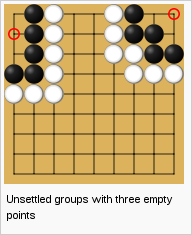
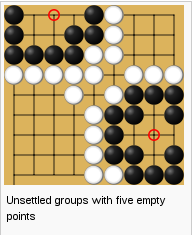Def. 5: A region is a group along with some additional unfilled space.
Def. 6: A critical point in the unfilled space of a region is a point that if and only if filled, would make the extended group (original group of the region, along with the newly filled point) a connected group with two or more eyes.
Prop. 3: A group in a region is “alive,” if it has two or more critical points.
Proof: Assume it’s the opposing color to move. The best move would be to deny one of the critical points. Yet there are other critical points, so therefore a response at one such point would create a connected group with two or more eyes, which cannot be captured by Prop. 2.

Prop. 4: A critical point, if it exists, has at least two liberties.
Proof: A point with zero or one liberty does not create new eyes upon filling the point, so it cannot be a critical point.

Thus, immediately, the enclosing group of L-shape and Z-shape spaces-of-four are alive, because there are two critical points in the unfilled space. The enclosing group of straight-line spaces-of-five-or-more are also alive, since there are even more critical points.

Def. 7: A critical tree in the unfilled space of a region is a set of points that can be arranged into a hierarchical tree, such that making moves along any complete path in the tree results in a connected group with two or more eyes, and making any other moves does not.
Prop. 5: A region with a critical tree of branching factor at least two at each level (a good tree), is “alive.” If all branches of the root have some child node with a single branch (a bad tree), then the region is “dead.” If only one subtree of the root is good and the remaining subtrees are bad, then the region is “unsettled.”
Proof: In the first case, since the branching factor is at least two, no matter what the opposing color does at each move, there is always another subtree remaining to complete a path. In the second case, then even if the group’s color makes the first move, at some level, the tree does not branch, and the opposing color would play the corresponding non-branched child, making it impossible for a complete path to be made by the group’s color. In the third case, if it’s the group’s color to move, then the “good” subtree would be chosen; if it’s the opposing color to move, also the “good” subtree would be chosen, but in this case, the opposing color occupies the root of the good subtree and denies a complete path to the group’s color.

Corollary 2: Prop. 3 is a special case of Prop. 5 with a one-level tree.

So we see, for instance, that the enclosing group of the spaces-of-four in the square shape is “dead,” since the branches of the critical tree consists of the two internal diagonals of the square shape, the two subtrees of which (both single-branching) are both “bad.”

Corollary 3: A group in a region may be “unsettled,” if the region has exactly one critical point.
Proof: This is a special case of Prop. 5 with a single “good” subtree of depth 1, and possibly some remaining subtrees from the root that may be good or bad. If the group’s color is first to move, then the critical point can be filled and the extended group cannot be captured by Prop. 2. However, if it is the opposing color to move, then the best move would be to deny the critical point with an opposing color stone. In order to capture that stone, the group’s color would have to exhaust all the liberties of the original critical point, thereby making it not a critical point in the resulting configuration by Prop. 4. Whether the new configuration is alive is undetermined as it depends on whether at least some of the other subtrees from the root are good.

In the case of the enclosing group of straight-line and L-shape spaces-of-three, as well as the pyramidal spaces-of-four, for example, there is only one branch from the root and it is a “good” subtree of depth 1. Therefore, by Prop. 5, these groups are “unsettled.”

* Incidently, “Go” potentially has an infinite number of variations, because it can be played under changes of the board topology and handicap stones. The axiomatic rules don’t need to change in that they are topologically agnostic. There are even 3D “Go” boards. Additionally, if multiple moves can be made per turn, the entire game also changes — for instance, you’d need to create three or more eyes to be alive if two moves can be made per turn, etc., all the more reasons to prove general results. (See also this.)