t-Mobile has these tiered refill cards for their prepaid mobile phones. The pricing table is here and reproduced below:

$10 for 30 minutes, expires in 90 days
$25 for 130 minutes, expires in 90 days
$40 for 208 minutes, expires in 90 days
$50 for 400 minutes, expires in 90 days
$100 for 1000 minutes, expires in 365 days

So which card should you buy? You could calculate a per minute cost and conclude that $100 for 1000 minutes is the most economical (plus it doesn’t expire for the longest time). Wrong!

It depends on how much you use the phone. The fact that the minutes expire makes the prepaid plan a virtual monthly plan in the regime where you do not use 1000 or more minutes per year, which is highly likely for people who choose prepaid phones to begin with (e.g. temporary visitors, odd occasions, emergencies, etc.). The constraint in that case is the expiration, not the number of minutes. If you blindly purchased $100 refills one after another, you’d have more and more unused minutes piling up. Sure, you could still use them, but even at $0.10/min. it is expensive compared to a straight monthly plan if you really mean to call that much. Of course you don’t, so now what?

The trick is time-sharing. (Never thought this phrase would pop up in this context.) Let’s re-write the table in terms of how much you get for $1, both minutes of call, and days of non-expiry:

$10: 3 min., 9 days / $1
$25: 5.2 min., 3.6 days / $1
$40: 5.2 min., 2.25 days / $1
$50: 8 min., 1.8 days / $1
$100: 10 min., 3.65 days / $1

We see that the $25, $40, and $50 refills are good for nothing! Why would anyone buy those? A rational person should only buy the $10 and $100 refills in some combination: $10 for when the account is about to expire but there are plenty of minutes, and $100 for when running low on minutes. The “proof” is as follows:

We really care about paying the lowest per minute cost for the minutes actually used. To that end, if we divide the purchase between the \(N\) refill options by the weights \(w_i\), \(i=1,…,N\), and every $1 of the \(i\)th refill option pays for \(m_i\) minutes and \(d_i\) days, then, we want

maximize \(\sum_{i=1}^N w_i d_i\) (equivalently, maximize \(\sum_{i=1}^N w_i m_i\))
subject to \(\sum_{i=1}^N w_i m_i / \sum_{i=1}^N w_i d_i = L\)
and \(\sum_{i=1}^N w_i=1\)

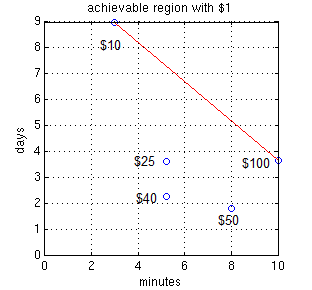where \(L\) is the minutes per day that we know we use. We don’t even need to solve this explicitly. The plot shows that every point in the pentagonal region below the red line is achievable with $1, and for any given constraint \(L\), the outer boundary on the red line itself solves the optimization (i.e. is the most economical), and this is done by using only the $10 and $100 refills. Here we assumed infinitely divisible refills. By using the heuristic of when to buy which refill above though, we tend toward the average \(L\) by construction so we are always at the right operating point.

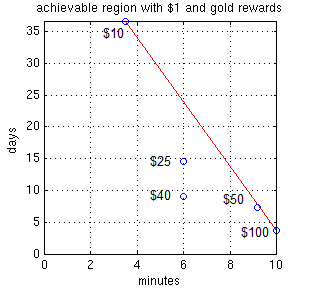The same analysis can be carried over to the “gold rewards” tier, which you get when you purchase the $100 refill and keep the account from expiring year after year (this is what you should do anyway, so even better). The new plot is different but the conclusion is the same, though the $50 refill looks competitive this time.

(For reference, the monthly cost of such a “virtual monthly plan” ranges from an incredible $0.82/mo. for 3 min./mo. — keeping the account active, basically — to $8.22/mo. for 82 min./mo. For more than 82 min./mo., the cost goes up at a rate of $0.10/min. of course. Unfortunately, you cannot buy “negative” refills, otherwise you could do better even in that regime.)