This is fascinating. Most things that sound fascinating at first really are pretty boring, but this is a notable exception in quite a few years.

First there was a seminar (which I missed) with this kind of description

How grid cell neurons encode rat position

Recently it was discovered that neurons in an area of the cortex (called dMEC) of rats, fire on every vertex of a regular triangular lattice that tiles 2-d space. These so-called “grid cells” efficiently encode rat position in a system that can be shown is analogous to a residue number system (RNS). By interpreting measured dMEC properties within an RNS framework, we can estimate the amount of position information stored within dMEC, and show how an RNS-like scheme is particularly well-suited to store and update positional information.

That tipped me off to this really amazing paper:
Microstructure of a spatial map in the entorhinal cortex by Hafting, Fyhn, Molden, Moser, and Moser.

It turns out, through experiments on rats, that in the “dorsocaudal medial entorhinal cortex” are a collection of neurons called “grid cells” that together ingeniously encode a coordinate chart for the rat to do internal path integration. The neurons respond when the rat is in certain positions in a standard environment — so what, you say. But no, if you plot the rat positions in the environment at which one particular neuron responds, the positions form a hexagonal lattice!

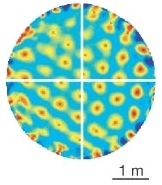What?

Neighboring cells have slightly shifted lattices for their positions of response, and there are other cells whose associated lattices are at a different angles or scales.

What good is this? Well, it implies a structurally coded representation of position. Suppose you had to encode a discretized 1D position, so a number between 1 and something, let’s say 15. You can use a sparse representation, which is to say, one neuron dedicated to respond to each of the 15 positions. You can use a binary code, and that would take 4 bits; the way to implement it might be a neuron that responds to positions 1-7, another one to positions 8-15, yet another one for positions 1-3, 8-11, another one for positions 4-7, 12-15, etc. That would take a total of 8 neurons. That’s pretty much an efficient representation. The way that it works in the dMEC is more like one neuron encodes all positions that are 1 (mod 3), another for 2 (mod 3), another for 0 (mod 3), another for 1 (mod 5), one for 2 (mod 5), and so on, for a total of 8 neurons again. These eight neurons repond to points on a lattice of distance 3 or a lattice of distance 5, and the response is narrowly confined. This is what the original seminar meant by residue number system encoding. The same extends to 2D, with the consequence that only on the order of log-of-the-number-of-positions neurons are needed, instead of on the order of the-number-of-positions, are needed to code a position. The advantage of a residue code over a binary (or n-ary) code is the possibility of using neural devices that have fairly similar properties (modulus 3, 5, etc.), instead of ones whose modulus scaling must bridge exponentially larger gaps (2, 4, 8, etc.).

This is about the most elegant representation of a coordinate chart that one can think of. Even decoding seems easy: just sum all the responses onto an unfolded chart — the hippocampus if I understand correclty, and choose the tallest peak.

There is a bit more complexity than described above, since the responses are not discretized in space, but are functions over a continuous space, and the residue arithmetic is not over a discrete set, either. I can’t find any experimental data on how responses of different dMEC neurons actually correlate, so how the coding works exactly is still speculation. But I can imagine this being much like random binning, and nested lattice Wyner-Ziv distributed rate-distortion coding. In fact, those are the first things that came to mind. With even a little bit of angular variance or half-phase lattice dithering, a small number of lattices would already be able to code for position with very low distortion by emulating random binning. I don’t think multiple rotated lattices of different scales (but non-nested) have been considered as a model for distributed rate-distortion coding. If properly chosen, the decoding complexity ought not to be that high. There is something to learn from the brain.