Any unitary matrix can be written as an exponentiated Hermitian matrix.

\(U=e^{iH}\), with \(H^{\dagger} = H\)

See this.

Why do people say they cannot describe why they like this movie — and for the record, I don’t –? I can describe exactly what it is. Strip away all the garbage and you are left with a picture of space itself. The experience is exactly like what you would get by gazing into the night’s sky and pondering the connection of man and universe. The movie just forces you to do that for nearly three hours. You fill in the void with your own dreams. That’s all. Some people fall asleep instead.

The creepy artistry sticks with you a while, but in terms of methodological novelty — and I use that term lightly — John Cage’s 4’33″ from 1952 predates it by 16 years.
(Read the article)

By art music I mean contemporary classical music. I could say that everything is wrong with it, but that’s probably too glib. Instead I’ll break it down into progressively deeper reasons.

1. The soundscape
Noise, texture, gesture over pitch, rhythm, harmony. You thought serialism was information poor. Well contemporary music is possibly worse.
(Read the article)

The movie is not about magical guitar playing, though there is that.

I understand this movie did not do well when released, and there were many arguments explaining this fact, from casting to promotion to target audience, all of which may be true. The one reason that isn’t often mentioned or accepted is that the story just isn’t told well enough. By this I mostly mean that after watching the movie, it is difficult to give a confident answer to the question of “What is this movie about?” I believe this is the central reason why the movie suffered despite its stunningly imaginative and bold artistry. By the end of this post it should be clear that the problems lie structurally. Spoilers ahead.
(Read the article)

Here is a problem from fakalin. Find the error in the following proof:

Let \(x^{x^{x\cdots}} = 2\). Then \(x^{x^{x\cdots}} = x^{x^{x^{x\cdots}}} = 2\). Substituting, we get \(x^2=2\) and \(x=\sqrt{2}\). Now let \(x^{x^{x\cdots}} = 4\). Similarly, \(x^{x^{x^{x\cdots}}} = 4\), \(x^4=4\) and \(x=\sqrt{2}\). But then \(2=x^{x^{x\cdots}}=4\) and \(2=4\).
(Read the article)

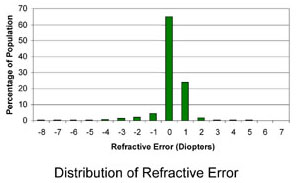According to this distribution, the mild amount of hyperopia (far-sightedness) I have in both eyes is in statistically acceptable ranges, and is easily corrected optically. Even without correction, this amount of hyperopia — unlike myopia — is such that I could and did get away with normal accommodation. After a visit to a very thorough ophthalmologist, though, I found out that refractive error was the least interesting thing about my vision, and as a result I finally have answers to everything that I had wondered about for years. For example, now I know why it was more difficult for me to see those Magic Eye images.
(Read the article)

I tend to reject the classification of languages onto the analytic-synthetic spectrum. I don’t think such a spectrum exists beyond a superficial level. Recall that this classification depends on the morphemes-per-word ratio, and as such, depends on the putative existence of “words”, i.e., that there are so-called bound morphemes making up multi-morpheme words in synthetic languages. What makes these morphemes especially more “bound” in synthetic languages? The fact that even in a purely analytic language, free morphemes are not really free in the sense that they must be arranged in some order with some grammar to make meaning, suggests that there is really no fundamental difference between analytic and synthetic languages. All morphemes are bound to one degree or another. Whether they can be uttered in isolation is more about function.
(Read the article)

\(A\) and \(B\) are two square matrices. The eigenvalues of \(AB\) and \(BA\) are the same.

Proof: Suppose \(\lambda\) and \(v\) are an eigenvalue and the corresponding eigenvector for \(AB\), so that \(ABv = \lambda v\). Let \(q = Bv\). Then \(Aq = \lambda v\), so \(BAq = \lambda Bv = \lambda q\). So \(\lambda\) is also an eigenvalue of \(BA\), and its associated eigenvector is \(q = Bv\).

This BSO concert featured some pieces by Miaskovsky and Knussen (Knussen was also the conductor). I must admit that I did not fully comprehend it (fell asleep midway through Miaskovsky), and so went back to review, mainly this and this — the last two on the program were probably audience appeasement and brought lesser difficulty.

I’ll go out on a limb and say those “difficult” pieces weren’t accessible for a lot of people, judging from the live reaction. In a pre-recorded discussion, Knussen said something about this: that they weren’t aimed for accessibility, something which he disdains, but they were also not deliberately obfuscating. This is already a better sentiment than expressed in Copland’s article on “modern music” (which this concert was), but I still take great issue with this, on the grounds of the purpose of art and especially, art performance.
(Read the article)

This tool, pkfix, is so useful, I cannot even breathe right now. Some old PostScript files generated through the LaTeX/DVI process use bitmap fonts, and when converted to PDF, their texts look ugly or fuzzy, and are unsearchable. People put these up without the source, and it appeared we were out of luck.

Not so! Using pkfix, the bitmap fonts are replaced in the PS file by their equivalent vector font counterparts on the system. Once that’s done, and the PS converted to PDF, the text looks sharp with that freshly typeset look. Search also works.