Here’s a problem posed to me by a friend:

Consider an equilateral triangle ABC with edge length 1. At each vertex is an object that is capable of movement at exactly speed 1. Beginning at time 0, each of the three objects moves toward its initial adjacent neighbor object, as in a game of pursuit. Of course, by symmetry, the objects will meet at the incenter of ABC. The question: how far will they have traveled?

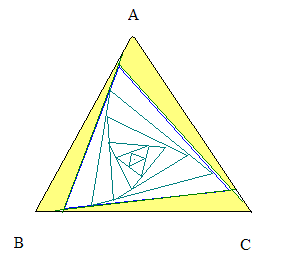The paths followed by the objects at first seem non-trivial, but in fact turn out to be nice. We will come back to this, but for the problem, the exact paths are irrelevant. We just need to find the amount of time it takes the objects to meet. The key part of the solution is to realize that, due to symmetry, the three objects always define an equilateral triangle at any time. Furthermore, their direction of motion is always along the edges of such a triangle, at speed v=1.

What we have is then a shrinking and rotating equilateral triangle that eventually decays to a point. Let us characterize this process.

At time \(t\), let \(s(t)\) be the length traveled by one of the objects. Let \(l(t)\) be the edge length of the triangle. Let \(A(t)\) be the area of the triangle. Then we have several relationships:

• \(\frac{ds}{dt}=1\)
• \(A(t)=\frac{\sqrt{3}}{4} l(t)^2\), and \(\frac{dA}{dt} = \frac{\sqrt{3}}{2} l(t) \frac{dl}{dt}\)
• By geometry, \(A(t+\Delta t) – A(t) = -3 (l(t) – \frac{ds}{dt} \Delta t) \frac{\sqrt{3}}{4} \frac{ds}{dt} \Delta t + o({\Delta t}^2)\), thus \(\frac{dA}{dt} = -3 \frac{\sqrt{3}}{4} l(t)\)

Combining: \(-\frac{3}{4}\sqrt{3} l(t) = \frac{\sqrt{3}}{2} l(t) \frac{dl}{dt}\)
\(\frac{dl}{dt} = -\frac{3}{2}\). Integrating with boundary conditions, we get \(-\frac{3}{2}t_f = -1\), \(t_f = \frac{2}{3}\), and since speed is 1, \(s(t_f) = t_f = \frac{2}{3}\). This is how far the object travels.

Finally, since the process is self-similar at every step along the path, the path of the object must be a logarithmic spiral. Furthermore, since the linear speed on the path is constant, the angular speed must be exponentially increasing (in angle) toward the center of the spiral.

To solve for this spiral explicitly, we have \(\frac{dr}{dt}=\frac{dr}{d\theta} \frac{d\theta}{dt} = \frac{\sqrt{3}}{3} \frac{dl}{dt} = -\frac{\sqrt{3}}{2}\).
\(\frac{dr}{d\theta} = -k \exp(-k \theta)\), so \(\frac{d\theta}{dt} = \frac{\sqrt{3}}{2k} \exp (k\theta)\), and \(\theta(t) = -\frac{1}{k} \ln(-\frac{\sqrt{3}}{2}t + C)\). Plugging into \(r(\theta) = \exp(-k\theta)\) and applying the boundary condition \(r(\theta_0) = \frac{\sqrt{3}}{3}\), we get \(r(t) = -\frac{\sqrt{3}}{2}t + \frac{\sqrt{3}}{3}\).
Next, \(\int_{\theta_0}^\infty r(\theta) d\theta = \frac{\sqrt{3}}{3k} = \frac{2}{3}\), so \(k=\frac{\sqrt{3}}{2}\) and \(\theta(t) = -\frac{2\sqrt{3}}{3} \ln(-\frac{\sqrt{3}}{2}t + \frac{\sqrt{3}}{3})\).